W poprzednim artykule opisałem, jak zacząć przygodę z Rustem i WebAssembly. Stworzyliśmy wizualizacje w przeglądarce planszy, składającej się z przypadkowo dobranych pól spośród 4 dostępnych typów. W tym artykule rozszerzę wcześniej napisany program o :
- Wyszukiwanie trasy pomiędzy dwoma zadanymi punktami A i B,
- Logowanie na konsolę po stronie Rusta, którego efekty będą widoczne w konsoli przeglądarki.
- Zmianę punktu wyjściowego i wejściowego dla przeszukiwanej ścieżki.
Dodanie Logowanie
Zacznijmy więc od udostępnienia możliwości logowania informacji do konsoli w przeglądarce. W poprzednim artykule używaliśmy wasm-bindgen crate, który umożliwia budowanie bindingów do i z Rusta. Wykorzystaliśmy go do udostępnienia struktur i funkcji napisanych po stronie Rusta, a konsumowanych po stronie JS.
Dzięki temu crate’owi możliwe jest także importowanie do Rusta (a dokładniej do WebAssembly) np: modułów, funkcji napisanych przez nas w JS.
Służy do tego konstrukcja językowa: extern "C" { }
Oraz atrybut #[wasm-bindgen(module = "./nazwa_modułu.js")]
Nas konkretnie interesuje możliwość logowania informacji w trakcie przetwarzania planszy, a dokładniej w trakcie poszukiwania ścieżki. By osiągnąć ten cel, możemy skorzystać z biblioteki web_sys, która udostępnia bindingi do WebAPI, wykorzystując do tego wasm-bindgen. Dzięki temu nie musimy sami pisać importów funkcji, ale wykorzystać gotowe do użycia.
W przestrzeni console crate’u web_sys znajdują się różne funkcje, które powiązane są w funkcja log po stronie JS, czyli umożliwiają nam logowanie informacji do konsoli.
Dla przykładu odpowiednikiem funkcji console.log po stronie js jest funkcja web_sys::console::log_1()
By móc logować, wystarczy wywołać tę funkcje z odpowiedni stringiem:
web_sys::console::log_1(“Achtung”.into());
Zmiana punktu początkowego i końcowego
Przypomnę pokrótce, co było celem poprzedniego artykułu. Było nim stworzenie planszy, która dookoła została otoczona ścianami, a wewnątrz planszy w sposób przypadkowy zostały rozlosowane typy pól, takie jak: wolne pole, ściana, woda i las.
Kolejnym krokiem jest wyznaczenie ścieżki pomiędzy dwoma wyznaczonymi przez nas punktami. W poprzednim artykule te punkty były podane na sztywno w kodzie.
Zanim przejdziemy do budowania ścieżki, fajnie by było mieć możliwość zmiany punktu początkowego i końcowego.
W html zostały dodane 4 inputy typu number. Natomiast ustawianie wartości początkowy zostało zrealizowane po stronie kod JS:
document.getElementById("start_x").value = START_X;
document.getElementById("start_x").max = WIDTH;
document.getElementById("start_y").value = START_Y;
document.getElementById("start_y").max = HEIGHT;
document.getElementById("end_x").value = END_X;
document.getElementById("end_x").max = WIDTH;
document.getElementById("end_y").value = END_Y;
document.getElementById("end_y").max = HEIGHT;
Następnie przycisk został wyposażony w event handler dla eventu click. Jako pierwszy krok przerysowuje całego naszego Boarda.
Wiem, że nie jest to najlepsze rozwiązanie. Lepszym byłoby odtwarzanie kafelków pod oryginalnym pathem, ale na potrzeby tego artykułu zostanie to zrealizowane w następujący sposób. Zrobiłem to, by nie wprowadzać dodatkowego utrudnienia do artykułu.
W linijce 3 zostaje wywołana funkcja search, która pochodzi z Webassembly. Jako, że zarówno startPoint, endPoint i Board są zmiennymi, które wskazują na pamięć po stronie WebAssembly, operacje będą wykonywane po stronie WebAssembly.
calculateButton.addEventListener("click", event => {
drawCells(board);
const {startPoint, endPoint} = createPoints()
const result = search(startPoint, endPoint, board)
const cells = new Uint32Array (memory.buffer, result.all_path(), result.count() * 2);
drawPath(cells, result.count() * 2)
});
Przesyłanie ścieżki
W pierwszym artykule pokazałem, że jeśli chcemy się dostać do wektora typów prostych (w tamtym wypadku były to numeric) reprezentujących typ pola, musimy mieć:
- Dostęp do pamięci przechowującej nasz wektor. Jako, że wektor jest w pamięci WebAssembly, to dostęp mamy dzięki memory.buffer.
- Adres wektora. O to już musimy zadbać sami.
- Typ danych, które przechowujemy.
- Długość wektora.
Do przesłania wskaźnika stworzyłem metodę, która zwraca nam wskaźnik na początek wektora.
pub fn all_path(&self) -> *const Point {
self.path.as_ptr()
}
W poprzednim przypadku wektor przechowywał wartości 8 bitowe. Dlatego wybraliśmy Uint8Array by móc przeiterować wektor i odtworzyć pola. Dla potrzeby tego kursu załóżmy, że wektor ścieżki będzie przechowywał n punktów, którego składowymi będą wartości 32 bitowe. Jako, że punkt zawiera dwie wartości, będziemy potrzebować przeiterować 2 * n komórek. Zamiast Uint8Array wykorzystamy inną funkcję Uint32Array.
new Uint32Array (memory.buffer, result.all_path(), result.count() * 2);
Rysowanie będzie proste – wystarczy przeiterować po 2n elementach. W każdej kolejnej iteracji należy zdjąć dwa kolejne elementy. Dla przykładu element 11 para to odpowiednio 22 i 23 int licząc od początku wektora.
Pathfinding
Wszystko po stronie JS jest gotowe. Teraz zajmijmy się rzeczami związanymi z WebAssembly, a dokładniej z Rustem. Mając zadany punkt S i punkt K oraz planszę, składającą się z różnych pól, chcemy znaleźć najtańszą drogę dotarcia z punktu S do punktu K.
Najtańszą? Co to oznacza?
Mamy 3 rodzaje pól, po których można się porusząć:
- Wolne – koszt przejścia 1
- Drzewo – koszt przejścia 3
- Woda – koszt przejścia 5
Przejście przez ściany jest niemożliwe. Do znalezienia ścieżki wykorzystam algorytm A*., który działa w następujący sposób.
- Definiuje 2 kolekcje:
- Pola do przeszukania
- Pola, które już przeszukaliśmy
- Do kolekcji do przeszukania dodaje pole startu
- Wyciągam z kolekcji te pole, które ma najmniejszy scoring (koszt łączny):
- Scoring to suma kosztu dotarcia do tego miejsca oraz odległości do celu
- Sprawdzam, czy osiągnęliśmy punkt końcowy. Jeśli tak, to zwracamy ścieżkę.
- Sprawdzam, czy punkt, który przetwarzam, był już odwiedzony.
- Jeśli tak – skaczę do 3.
- Jeśli nie – to dodaje go do kolekcji już przeszukanych.
- Dla danego punktu wyszukuje wszystkie pola sąsiadujące z nim. Dodaje je od kolekcji do przeszukania Skacze do punktu 3.
Ścieżka przeszukania
By móc wyświetlić pełną ścieżkę od punktu A do punktu B, musimy mieć wektor zawierający punkty, po których się poruszaliśmy. Dodatkowo potrzebny nam jest koszt sumaryczny.
Do przechowywania tych informacji użyjemy struktury:
#[wasm_bindgen]
#[derive(Clone, Debug)]
pub struct SearchState{
pos: Point,
path: Vec,
h: f64,
g: f64,
f: f64
}
Pos to pozycja aktualna punktu. Path to wszystkie punkty, po których się poruszaliśmy, by tu się dostać, łącznie z punktem aktualnym. G to koszt dotarcia. H to odległość od punktu końcowego. F to sumaryczna wartość G + H.
Co one oznaczają?
G to całkowity koszt dotarcia do tego miejsca. Mamy 4 rodzaje pól na planszy o różnym koszcie wejścia:
- Ściana – niemożliwe jest wejście na dane pole,
- Wolne pole – koszt wejścia 1,
- Las – koszt wejścia 3,
- Woda – koszt wejścia 5.
- Koszt całkowity to suma wszystkich kosztów wejść z każdego do tej pory odwiedzonego pola.
H to odległość z aktualnego pola do miejsca docelowego. Wyliczona dzięki metryce. Do tego mogą służyć różne metryki, ale ja wykorzystam metrykę euklidesową liczoną według wzoru:
Sqrt((x2 - x1)^2 + (y2 - y1)^2)
Przykład
By lepiej zobrazować, jak działa ta część algorytmu posłużę się przykładem.
Mamy plansze składającą się z 4 pól.

Punkt (0,0) to punkt startowy. Punkt (1,1) punkt końcowy. Punkty o współrzędny (1,0) to las, a punkt (0,1) to woda.
Zaczynamy w punkcie (0,0). Jego koszt dotarcia wynosi 0, bo w nim jesteśmy, a odległość do celu wyliczymy ze wzoru: sqrt(2). Czyli F będzie wynosiło sqrt(2).

Analizujemy kolejne pola. Jeśli chcemy pójść do punktu (1,0) z punktu (0,0), to koszt wejścia na pole wynosi 3, bo znajduje się tam las. G wynosić będzie sumaryczny koszt podróży do tej pory, czyli 0 (koszt wejścia na pole startu) + 3 (koszt wejścia na pole (1,0). Odległość według metryki wyniesie 1. Koszt F będzie wynosić 4.
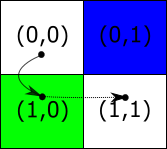
Analogicznie można wyliczyć wartości dla przejścia (0,0) na (0,1) lub dla przejścia pełnej ścieżki (0,0) -> (1,0) -> (1,1)
Dlaczego to robimy w taki sposób?
Chcemy znaleźć najbardziej korzystną ścieżkę dojścia z punktu A do punktu B, biorąc pod uwagę koszty podróży. Decyzje praktycznie podejmujemy przeszukując planszę krok po kroku i podejmując decyzje iteracja po iteracji.
Struktura search_state ma nam pomóc przy wyborze najlepszej opcji. O tym świadczy najniższa wartość parametru F.
Co to znaczy dla nas?
Dysponujemy listą punktów do przeszukania. Punkty do przeszukania powiązane są z historią dojścia do tego miejsca, w tym z kosztem podróży. Mając do dyspozycji wartość F wiemy, jaki jest sumaryczny koszt podróży do tej pory, plus jego przewidywany koszt bez uwzględnienia wartości faktycznych podróży.
Cel: Wystarczy wybrać ten search_state, który ma najmniejsze F.
Wybór punktu do analizy
Za każdym razem wybieram to pole, które ma najmniejszy scoring, czyli koszt łączny.
Idąc za przykładem zawsze zaczynamy w punkcie startowym, znajdujemy jego sąsiadów i z tych sąsiadów wybieramy tę najlepszą opcję – najmniejszy scoring. Co oznacza, że chcemy dotrzeć do celu minimalnym kosztem.
Dopóki nie dotrzemy do celu, to dokładamy kolejne punkty do odwiedzenia. Z tej listy zawsze wybieramy najlepszą opcję do wyboru.
Miejsca do odwiedzenia przechowuję w
let mut fringe:Vec= Vec::new();
Słowo kluczowe mut pozwala mi modyfikować wektor, czyli dokładać do niego nowego punkty do odwiedzenia.
Scoring, czyli łączny koszt podróży może być liczbą rzeczywistą. Do jego reprezentacji – jak wcześniej mogłeś zauważyć – używam zmiennej typu f64.
Chcąc wybrać te z najmniejszym scoringiem, muszę zapewnić dwie rzeczy:
- Możliwość porównywania
- Możliwość sortowania
- w strukturze SearchState.
Porównywanie i sortowanie
Kiedy dwie struktury SearchState są identyczne? Gdy ich koszt, czyli F, jest identyczny.
By móc je porównać, muszą implementować trait: partialEq
impl PartialEq for SearchState {
fn eq(&self, other: &SearchState) -> bool {
self.f == other.f
}
}
By móc je posortować, muszą implementować trait: partialOrd
impl PartialOrd for SearchState {
fn partial_cmp(&self, other: &SearchState) -> Option {
self.f.partial_cmp(&other.f)
}
}
Wykorzystuję do tego fakt, że typ f64 implementuje te dwa traity, więc mogę wywołać odpowiednie metody lub użyć operator porównania.
Następny krok jest prosty – możemy wykorzystać metodę sort_by wektora oraz lambdę, która porówna nam dwie struktury i powie, która większa, która mniejsza lub czy są równe. Dzięki temu możliwe będzie ich ułożenie.
fringe.sort_by(|a,b|a.partial_cmp(&b).unwrap());
Lambdę definiujemy poprzez konstrukcję |a,b| a to, co po niej następuje, to wywołanie porównania. Nie wnikając w to, czym jest Option, robię unwrap, by wyciągnąć z niego odpowiedź, czy a jest : mniejsze, większe lub równe.
Sortowanie malejące
Problem, który mam teraz: wektor jest posortowany w zły sposób. Musiałbym odwrócić kolejność, robiąc reverse lub stosując prosty trick, który zaraz pokażę.
Sortowanie odbywa się za pomocą partial_cmp, które zdefiniowałem wcześniej. To nam zwraca jedną z trzech opcji: Ordering::Less, Ordering::Equal, Ordering::Greater.
Stworzę więc funkcję reverse, która przyjmie wynik porównania i go odwróci.
fn reverse(ordering: Ordering) -> std::cmp::Ordering{
match ordering{
Ordering::Less => Ordering::Greater,
Ordering::Greater => Ordering::Less,
Ordering::Equal => Ordering::Equal,
Dzięki czemu sort_by ułoży nam w odpowiedniej kolejności następne punkty do analizy.
fringe.sort_by(|a,b| reverse(a.partial_cmp(&b).unwrap()));
Wspomnę tylko, że sort_by modyfikuje zawartość wektor.
Znajdowanie sąsiadów
Chcemy przeszukać wszystkie sąsiadujące z danym punktem pola w poszukiwaniu tych, które nie są ścianami:
Wektor przeszukania definiuje w następujący sposób:
let directions:Vec< (i32, i32)> = vec![(-1,0), (-1, 1), (0, 1), (1, 1), (1,0), (1, -1), (0, -1), (-1, -1)];
Przeszukanie punktów wektora odbywa się poprzez
for direction in &directions {
}
Dla punktu, który nie jest ścianą i nie jest poza planszą, obliczamy wcześniej wspomniane parametry:
let mut path = state.current_path().clone(); path.push(new_pos.clone()); let cost = state.cost() + calculate_cost(&cell); let distance = new_pos.dist_to(&end_point);
Jeśli pamiętacie artykuły o pożyczaniu oraz przenoszeniu, to klonowanie (clone()) nie wyda się wam niczym nowym. Na podstawie punktu, który istnieje, tworzę własne kopie ścieżki. A tam gdzie chcę tylko obliczyć koszt i dystans, przekazuje pożyczenie, gdyż nadal w obrębie tej funkcji chce z nich korzystać.
Algorytm A*
Bazując na powyżej przedstawionych rzeczach budujemy ostateczny algorytm:
#[wasm_bindgen] pub fn search(start_point: &Point, end_point: &Point, board: &Board) -> Option{ log!("Starting"); let mut fringe:Vec = Vec::new(); let mut closed:Vec = Vec::new(); fringe.push(create_initial_state(&start_point, &end_point)); let result = loop { if fringe.is_empty() { break None; } fringe.sort_by(|a,b| reverse(a.partial_cmp(&b).unwrap())); let state: SearchState = fringe.pop().unwrap(); if state.current_pos().eq(&end_point){ break Some(state); } if closed.contains(state.current_pos()) { continue; } closed.push(state.current_pos().clone()); fringe.append(&mut get_successors(&state, &end_point, &board)); }; log!("Ending"); result }
Wynik działania algorytmu:
Podsumowanie
Dzięki WebAssembly da się całkiem łatwo wykorzystywać potęgę Rusta do budowania aplikacji, które potem będą uruchamiane w przeglądarce.
Dzięki temu można skupić się na tworzeniu wysokopoziomowych, ergonomicznych aplikacji w JS, a niskopoziomowe, skupiające się na kontroli, bezpieczeństwie pamięci komponenty budować w Rust. Nie znaczy to, że wszystko należy pisać w ten sposób. Ale jeżeli potrzebujemy tego bezpieczeństwa, mamy taką możliwość.
Jednak różnice między tymi dwoma światami są zauważalne. WebAssembly nie jest magicznym narzędziem – to programista musi wiedzieć, jakie są różnice w typach oraz w jaki sposób można je na siebie mapować. Dla przykładu: JS numeric może być typem docelowym dla dużej ilości typów prostych po stronie Rust: i32,u32, u8,i8, f64, …. Mogą powstawać liczne problemy przy przesyle zmiennych i należy napisać odpowiedni kod defensywny i obsłużyć błędy z tym związane.







